Ẩn dữ liệu và chia sẻ thông tin

I) Phương pháp chia sẻ thông tin mật của Shamir

Giả sử ta muốn chia sẻ một thông tin mật S cho n người

•  Ta muốn phải có ít nhất là k người (k ≤ n) thì

mới tái tạo được S

•  Còn nếu có ít hơn k người thì sẽ không tái tạo

được S (cũng không biết gì về S)

•  Bài toán chia sẻ thông tin mật: chia thông

tin mật S thành n phần S1, S2, … , Sn sao cho:

•  Với ít nhất là k phần bất kỳ (k ≤ n) thì sẽ tái tạo

được S

•  Với ít hơn k phần thì sẽ không biết gì về S

Phân chia thông tin mật

Input:

• Thông tin mật S (một con số)
• Số phần cần chia n
• Ngưỡng k

Quá trình thực hiện:

• Tạo hàm f là một đa thức bậc k − 1 sao cho f(0) = S
• S1 = (1, f(1)) , S2 = (2, f(2)) , S3 = (3, f(3)) , …

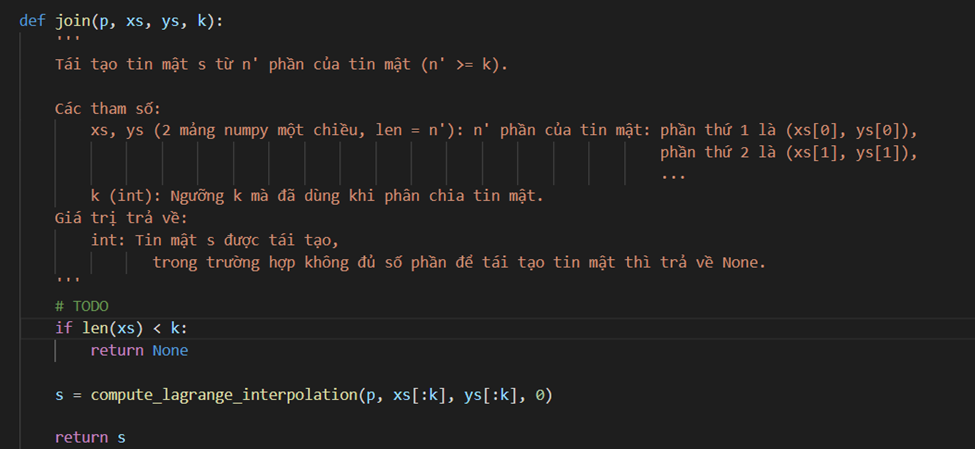
Tái tạo thông tin mật

Input:

• Ngưỡng k
• n’ phần của thông tin mật (n′ ≥ k)

Quá trình thực hiện:

• Tái tạo hàm f (đa thức bậc k − 1) từ k phần trong n′ phần
• S = f(0)

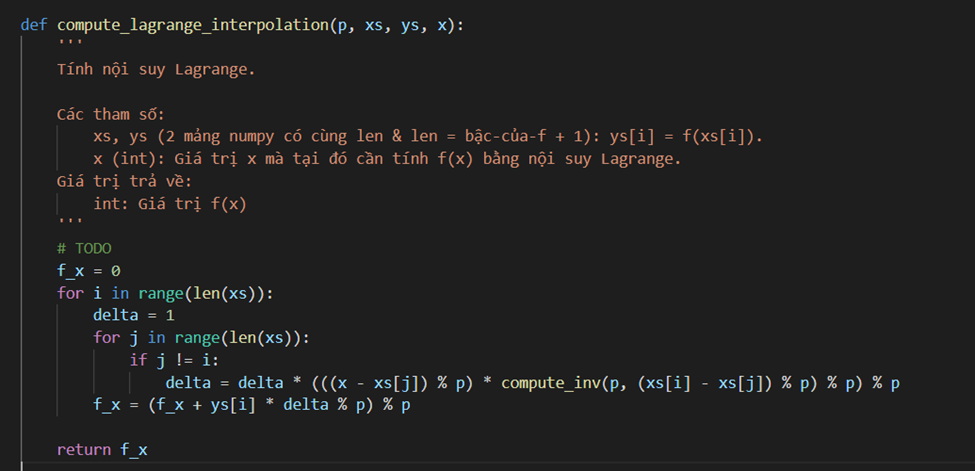
Tái tạo hàm f (đa thức bậc k − 1) từ k phần của thông tin mật

Tìm hàm đa thức bậc k − 1: từ k điểm x1, y1 , … , (xk, yk) với yi = f(xi) → k phương trình, k ẩn:

• (a_k−1)x1^k−1 + (a_k−2)x1^k−2 + ⋯ + a0 = y1
• (a_k−1)x2^k−1 + (a_k−2)x2^k−2 + ⋯ + a0 = y2
• …
• (a_k−1)xk^k−1 + (a_k−2)xk^k−2 + ⋯ + a0 = yk

Giải -> Dùng phương pháp nội suy Lagrange

Nội suy Lagrange

Ví dụ, tìm hàm f (hàm đa thức bậc 3) biết:
<= f(5) = 3
<= f(7) = 2
<= f(12) = 6
<= f(30) = 15

Ta chỉ cần tìm một hàm: (i) bậc 3, và (ii) đi qua 4 điểm ở trên

f(x) = 3δ5(x) + 2δ7(x) + 6δ12 =(x) + 15δ30(x)

với δi(x) là một hàm bậc 3 và δi(x) =

• 1 nếu x = i
• 0 nếu x ∈ 5,7,12,30 − {i}
• “bất kỳ” trong những trường hợp khác

δ5(x) =(x − 7)/(5 − 7) (x − 12)/(5 − 12) (x − 30)/(5 − 30)

Ví dụ

S = 6, n = 3, k = 2

Phương pháp Shamir:

• Bước 1: tạo hàm f là một đa thức bậc nhất sao cho f(0) = S. Ví dụ, f(x) = −0.5x + 6
• Bước 2: S1 = (1, f(1)), S2 = (2, f(2)), S3 = (3, f(3))

II) Tại sao áp dụng trường hữu hạn lại giải quyết các vấn đề trên.

• Phương pháp Shamir với trường hữu hạn: giải quyết vấn đề biểu diễn số thực không chính xác và tràn số khi tính toán trên máy tính

Một giải pháp: dùng trường hữu hạn

•  Một trường (field) là một tập hợp mà trên đó:  Các phép cộng, trừ (cộng với số ngược dấu), nhân, chia (nhân với số nghịch đảo) được định nghĩa (kết quả của những phép tính này cũng phải nằm trong tập hợp của trường → có tiềm năng để tránh vấn đề tràn số)
• Và có tính chất như những phép tính trên số thực
• Số nguyên không phải là một trường vì có những số nguyên khi chia cho nhau thì kết quả không phải là số nguyên
• Số thực là một trường có vô số phần tử
• Máy tính chỉ có thể biểu diễn được một số lượng hữu hạn phần tử
• Có trường nào có hữu hạn số phần tử và đủ để máy tính có thể biểu diễn không.

      Trường nào là trường hữu hạn?

•  Xét tập hợp Z100 gồm 100 số nguyên 0, 1, …, 99 với các phép toán được định nghĩa như sau:
•  a cộng b: a + b mod 100
•  a nhân b: a × b mod 100
• a trừ b: a cộng −b với −b ∈ Z100 và −b cộng b = 0
•  a trừ b: (định nghĩa tương đương: a − b mod 100
•  a chia b: a nhân b −1 với b −1 ∈ Z100 và b −1 nhân b = 1
•  Z100 có phải là một trường?
• Số nghịch đảo của 3?
• 67
• Số nghịch đảo của 5?
• Không có → Z100 không phải là một trường

• Người ta đã chứng minh được: Zp là một trường khi và chỉ khi p là số nguyên tố
•  Dùng trường Zp cho phương pháp của Shamir sẽ tránh được vấn đề tính toán không chính xác trên máy tính
• Chọn p đủ nhỏ để máy tính có thể biểu diễn được p phần tử của trường
• Chọn p đủ lớn để tránh vấn đề trường có quá ít phần tử, kẻ tấn công có thể thử từng phần tử
• Tin mật S và số phần n phải là số nguyên ∈ [0, p)
• Thật ra, trong bài báo gốc của Shamir là dùng trường hữu hạn Zp